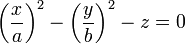.
A Gallery of Famous Surfaces montre et explique quelques surfaces mathématiques parmi les plus connues. On peut faire tourner toutes ces surfaces pour les voir sous tous les angles. Très joli site!
11 avril 2009
Antonio Gaudi
Le recours des architectes aux sciences mathématiques est guidé depuis les civilisations anciennes par des besoins pratiques,utilitaires et plus encore aujourd'hui,esthétiques .
De nos jours, Oscar Niemeyer, Santiago Calatrava sont connus pour les courbes mathématiques que le béton leur a permis de réaliser.
"Ce n'est pas l'angle droit qui m'attire, ni la ligne droite, dure, inflexible, créée par l'homme. Ce qui m'attire, c'est la courbe libre et sensuelle, la courbe que je rencontre dans les montagnes de mon pays, dans le cours sinueux de ses fleuves, dans la vague de la mer, dans le corps de la femme préférée. De courbe est fait tout l'univers,l'univers courbe d'Einstein.»
a dit l'architecte brésilien Oscar Niemeyer
Le parcours d'Antonio Gaudi est plus atypique :
De nos jours, Oscar Niemeyer, Santiago Calatrava sont connus pour les courbes mathématiques que le béton leur a permis de réaliser.
"Ce n'est pas l'angle droit qui m'attire, ni la ligne droite, dure, inflexible, créée par l'homme. Ce qui m'attire, c'est la courbe libre et sensuelle, la courbe que je rencontre dans les montagnes de mon pays, dans le cours sinueux de ses fleuves, dans la vague de la mer, dans le corps de la femme préférée. De courbe est fait tout l'univers,l'univers courbe d'Einstein.»
a dit l'architecte brésilien Oscar Niemeyer
Le parcours d'Antonio Gaudi est plus atypique :
Gaudi est connu du grand public pour la construction de la grande cathédrale de Barcelone, la Sagrada familia (encore inachevée) à la fois plus aérienne et plus solide qu'aucune autre cathédrale.
Son pari architectural a pu être tenu grâce aux étonnantes propriétés de la courbe dénommée chaînette que forme une chaîne qu'on la laisse pendre en la tenant par ses deux extrémités . Ce sont donc les propriétés mathématiques et physiques de la chaînette (qu'il a découvertes empiriquement) qui ont permis à Gaudi de concevoir ses colonnes de soutien comme de très minces troncs .
Son pari architectural a pu être tenu grâce aux étonnantes propriétés de la courbe dénommée chaînette que forme une chaîne qu'on la laisse pendre en la tenant par ses deux extrémités . Ce sont donc les propriétés mathématiques et physiques de la chaînette (qu'il a découvertes empiriquement) qui ont permis à Gaudi de concevoir ses colonnes de soutien comme de très minces troncs .
Toute l'oeuvre de l'architecte catalan Antoni Gaudi est inspirée dans les formes, la géométrie (et les couleurs) de la nature .
L'un de ses biographes, Juan Bassegoda Nonell, dit:
"Il s'était aperçu que les architectes n'utilisaient que des formes qu'ils ont pu dessiner auparavant avec deux instruments : l'équerre et le compas. Au cours de toute l'histoire de l'architecture les formes des édifices ont été créées à partir de ces deux basiques qui permettent de dessiner des cercles, des triangles, des carrés ou des rectangles, qui dans l'espace se convertissent en prismes, pyramides, cylindres et sphères, qui donnent lieu aux piliers, aux toitures, aux colonnes et aux coupoles.
... il vit clairement que ces formes géométriques simples ne se trouvent pratiquement jamais dans la nature, qui, d'autre part, construit d'excellentes structures, accréditées par de larges siècles d'efficacité. La structure d'un arbre est d'une perfection rare, bien plus complexe et plus aboutie que les structures créées par les architectes .
Libellés : Art et mathématiques, Courbes ou surfaces mathématiques
16 février 2009
Bac à glaçons mathématique.
Cette image fait partie de l’exposition IMAGINARY organisée par l’institut Mathematisches Forschungsinstitut Oberwolfach.
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
14 février 2009
Structure hyperboloïde
En mathématiques, un hyperboloïde est une surface du second degré de l'espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s'étendre à l'infini.Les sections non triviales d'un hyperboloïde avec un plan sont des paraboles, des ellipses ou des hyperboles.On peut générer un hyperboloïde par rotation d'une droite oblique autour de l'axe. Cela permet, en pratique, de réaliser le coffrage de construction de certains châteaux d'eau et de certaines tours de refroidissement de centrales à partir d'éléments rectilignes, ce qui leur assure une certaine stabilité.Sur la photo ci-contre,on aperçoit clairement les renforcements rectilignes
La première structure hyperboloïde au monde - la tour de treillage de claire-voie d'acier située actuellement à Polibino en Russie (photo ci-dessous), construite pour l'exposition de Nijni Novgorod de 1896 - est l'œuvre de l'ingénieur et scientifique russe Vladimir Choukhov. Les structures hyperboloïdes ont été par la suite utilisées par beaucoup d'architectes réputés : Antoni Gaudí, Le Corbusier, Oscar Niemeyer.
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
Coeur mathématique
11 février 2009
Citron mathématique
Cette image fait partie de l’exposition IMAGINARY organisée par l’institut Mathematisches Forschungsinstitut Oberwolfach.
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
29 janvier 2009
La roulette de Pascal (cycloïde)
La cycloïde droite, aussi appelée roue d'Aristote ou roulette de Pascal, est la trajectoire d'un point fixé à un cercle qui roule sans glisser sur une droite . C'est un cas particulier de roulette.Un chewing-gum s'est collé au pneu du vélo de Missmath ; ça l'a un peu énervée mais ça l'a fait réfléchir ; clique sur l'image!
La cycloïde et le calcul de ses propriétés furent l'objet de défis constants entre mathématiciens, si bien qu'elle fut surnommée « l'Hélène des géomètres ».
Après Descartes, Pascal caché sous un pseudonyme-même les plus grands n'aiment pas sécher- offrit un prix à qui résoudrait deux problèmes liés à la cycloïde et au mouvement du pendule. En 1656-1659, Christian Huygens étudie ses propriétés isochrones et les applique à la conception d'une horloge marine - le pendule classique n'est pas fiable en mer à cause des grandes variations de l'amplitude de ses oscillations- ce qui le conduira à la détermination du « secret des longitudes»; merci à la cycloïde!
La cycloïde est aussi une courbe brachistochrone , c'est-à-dire qu'une cycloïde représente la courbe sur laquelle doit glisser sans frottement et sans vitesse initiale, un point matériel pesant placé dans un champ de pesanteur de sorte que son temps de parcours soit minimal parmi toutes les courbes joignant deux points fixés situés à des altitudes différentes. Autrement dit, c'est la courbe de descente la plus rapide pour aller d'un point A à un point B situé plus bas.
Les concepteurs de rampes de skate savent (peut-être ?) que la rampe la plus rapide a une forme de cycloïde .
A ski , sur une neige très glissante,vous arriverez plus tôt en B en empruntant la piste rouge en forme de cycloïde,même si cela monte un peu vers la fin.Libellés : Courbes ou surfaces mathématiques
24 janvier 2009
Cette image fait partie de l’exposition IMAGINARY organisée par l’institut Mathematisches Forschungsinstitut Oberwolfach.Libellés : Courbes ou surfaces mathématiques, Images mathématiques
17 janvier 2009
La cardioïde au fond de la casserole
Les mathématiques sont partout, même au fond des casseroles comme le prouve cette photo où apparaît une étonnante cardioïde. Je vous avais promis d'en reparler lors d'un précédent billet.Si je vous dis :
"Une caustique désigne en optique ou en mathématiques l'enveloppe des rayons lumineux subissant une réflexion ou une réfraction sur une surface ou une courbe.La cardioïde étant une caustique de cercle,cela explique que la forme dessinée au fond d'une casserole par la réflexion des rayons lumineux provenant d'une source ponctuelle proche du bord de la casserole soit une cardioïde",
vous ne serez peut-être pas totalement convaincu .
Si vous cliquez sur l'image ci-dessous, vous le serez sans doute davantage.
(L' applet ci-dessus nécessite l'application java)
Vous pouvez aussi découvrir la cardioïde dans votre bol de café au lait
Libellés : Courbes ou surfaces mathématiques, Images mathématiques, Infos et actualités
15 décembre 2008
Chaînette.
En mathématiques, la chaînette est une courbe plane transcendante, qui correspond à la forme que prend un câble (ou une chaîne) lorsqu'il est suspendu par ses extrémités et soumis à une force gravitationnelle uniforme (son propre poids).Le problème de la forme prise par un fil pesant flexible a intéressé très tôt les mathématiciens. Galilée pensait que cette forme devait être un arc de parabole, mais la preuve du contraire fut apportée en 1669 par Jungius, après une première remise en cause par Huygens en 1646.L’équation cartésienne de la chaînette est :
y(x) = a ch(x/a) où la fonction ch désigne le cosinus hyperbolique .
Sur cette photo de Saint-Louis-Missouri,l'arche est en forme de chaînette.
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
08 décembre 2008
Lemniscate ( de lemniscus,mot latin signifiant ruban)
Une lemniscate de Bernouilli est une courbe plane ayant la forme d'un 8. Elle possède deux axes de symétrie perpendiculaires. Ceux-ci se coupent en un point double de la courbe, également son centre de symétrie.La première lemniscate décrite le fut en 1694 par Jacques Bernoulli lors de ses travaux sur l'ellipse et ses variations. Il la baptisa lemniscus, qui est le mot latin signifiant ruban. Une lemniscate de Bernoulli, de foyers F et F’, est l'ensemble des points M vérifiant la relation MF * MF' = OF²
La lemniscate de Bernoulli est souvent considérée comme une courbe qui se parcourt sans fin. Cette caractéristique de la lemniscate serait à l'origine du symbole de l'infini (version toutefois contreversée).La lemniscate de Bernoulli dispute à la cardioïde le record du nombre d'appartenances aux diverses familles de courbes remarquables.
Pour en savoir plus sur la lemniscate de Bernouilli et tant d'autres courbes remarquables:le site mathcurve de Robert FERRÉOL est une véritable encyclopédie des courbes mathématiques
Source : Wikipédia
Libellés : Courbes ou surfaces mathématiques
29 avril 2008
Surfaces minimales
En mathématiques et en physique, une surface minimale est une surface minimisant son aire. Ce minimum est réalisé sous une contrainte : un ensemble de points, le bord de la surface, est d'avance déterminé. Si un cerceau est retiré d'une bassine d'eau savonneuse, un disque de liquide reste fixé. Un souffle dessus déforme légèrement le disque en une calotte sphérique. Si l'étude fait appel à la physique des liquides, le traitement mathématique utilise le langage des surfaces minimales.
Intuitivement, une surface minimale est une surface dont l'aire ou le volume ne peut qu'augmenter lorsqu'on lui applique une perturbation suffisamment petite. Les surfaces minimales forment donc l'analogue en dimension supérieure des géodésiques (courbes dont la longueur ne peut qu'augmenter sous l'effet d'une perturbation assez petite et assez localisée).
En 1744, Leonhard Euler (encore lui !) posait et résolvait le premier problème de surface minimale : trouver, entre toutes les surfaces passant par deux cercles parallèles, celle dont la surface était la plus petite. Il découvrit ainsi la caténoïde.
Intuitivement, une surface minimale est une surface dont l'aire ou le volume ne peut qu'augmenter lorsqu'on lui applique une perturbation suffisamment petite. Les surfaces minimales forment donc l'analogue en dimension supérieure des géodésiques (courbes dont la longueur ne peut qu'augmenter sous l'effet d'une perturbation assez petite et assez localisée).
En 1744, Leonhard Euler (encore lui !) posait et résolvait le premier problème de surface minimale : trouver, entre toutes les surfaces passant par deux cercles parallèles, celle dont la surface était la plus petite. Il découvrit ainsi la caténoïde.
Libellés : Courbes ou surfaces mathématiques, Histoire des mathématiques, Images mathématiques
03 janvier 2008
Papillon paramétré
x(t)=(sin5t)*(cost)
y(t)=(sin5t)*(sin4t)
0< t <2*Pi
Libellés : Courbes ou surfaces mathématiques, Récréation
31 décembre 2007
Bonne et heureuse année mathématique.
x(t) = sin(2t) - 6sin(5t)y(t) = ( cos(4t) )^5 - 1.1cos(t)
0< t <2*Pi
Ce fichier , créé avec Maple , peut aussi être obtenu avec une simple calculatrice graphique ou un grapheur en ligne comme celui- ci
(sélectionner bien sûr le mode paramétrique et régler la fenêtre de calcul comme il convient)
Libellés : Courbes ou surfaces mathématiques, Infos et actualités, Récréation
30 décembre 2007
Le paraboloïde hyperbolique
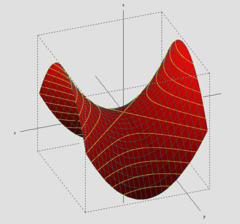
En mathématiques,un paraboloïde est une surface du second degré de l'espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie.
Certaines sections d'un paraboloïde avec un plan sont des paraboles. D'autres sont, selon le cas, des ellipses ou des hyperboles. On distingue donc les paraboloïdes elliptiques et les paraboloïdes hyperboliques.
La photo et le schéma nous montrent le paraboloïde hyperbolique.Dans un repère bien choisi, son équation est de la forme
La forme particulière de cette surface lui vaut le surnom de selle de cheval. On reconnaît,sur le schéma, en jaune, des hyperboles " horizontales " et en violacé, des paraboles "verticales "
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
15 novembre 2007
Cent cinquante courbes mathématiques.
A voir sur le site du palais de la découverte plus de 150 courbes algébriques , transcendantes ou ornementales et leur descriptif. Il est possible d'imprimer une fiche de chacune d'entre elles avec son descriptif.
Lien déniché par Le Math'Ador , l'excellent blog d'Olivier Legay
Lien déniché par Le Math'Ador , l'excellent blog d'Olivier Legay
Libellés : Courbes ou surfaces mathématiques, Infos et actualités
13 juin 2007
Images mathématiques: Escalier et spirale
Santiago de Compostelle (Espagne)
Libellés : Art et mathématiques, Courbes ou surfaces mathématiques, Images mathématiques
22 mai 2007
Images mathématiques : Escalier en colimaçon et spirale hyperbolique
La spirale hyperbolique a été étudiée par le physicien français Pierre Varignon en 1704. L'équation, en coordonnées polaires ,de cette spirale est tout simplement :
r=a/t (où a est un réel non nul)
L'équation r = a/t explique le nom de la courbe ; en effet y = 1/x est l'équation de l'hyperbole en coordonnées cartésiennes
La courbe permettant de déterminer les points de départ des coureurs sur un stade circulaire est une spirale hyperbolique
Libellés : Art et mathématiques, Courbes ou surfaces mathématiques, Images mathématiques
11 novembre 2006
Surfaces mathématiques : La bouteille de Klein
La bouteille de Klein est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle on ne peut pas définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein. Elle est étroitement liée au ruban de Möbius .
Libellés : Courbes ou surfaces mathématiques
10 novembre 2006
Diaporama mathématique extrait du site de Jean-François Colonna
(Cliquer sur l'image)
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
Dans la série : Images mathématiques
Les trajectoires des particules d'agrégats fractals bidimensionnels obtenus par collage de 50% de celles-ci lors de leurs collisions, dans un champ de gravitation vertical.Une boite rectangulaire (bidimensionnelle) verticale est immergée dans un champ de gravitation. A l'intérieur de celle-ci, il y a 24*34=816 particules massives. Au départ, elles remplissent uniformément la boite ; leurs vitesses sont aléatoires en direction et constantes en module. Au cours du temps, elles interagissent avec le champ de gravitation qui les attire vers le bas et par des chocs avec les parois ainsi qu'entre-elles. Dans ce dernier cas, la moitie des particules (choisies initialement au hasard) peuvent se coller les unes aux autres (elles apparaissent en blanc), alors que les autres rebondissent (elles sont coloriées en fonction de leurs positions initiales). Progressivement les particules collantes (blanches) forment un agrégat fractal au-dessus de la paroi inférieure de la boite. Les autres particules (colorées) sont soit libres a l'intérieur de la boite, soit piégées par l'agrégat. Enfin, les courbes montrent les trajectoires de chacune des particules depuis l'instant initial.
Libellés : Courbes ou surfaces mathématiques
06 novembre 2006
Clique
31 octobre 2006
Masse et gravité
Cliquez ici pour découvrir d'étranges attracteurs dont vous pouvez modifier la position à la souris
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
09 octobre 2006
Fantastiques images
Si , si , il y a des mathématiques dans ces images magnifiques !
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
07 octobre 2006
Surfaces mathématiques
Libellés : Courbes ou surfaces mathématiques, Images mathématiques
