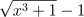04 mars 2010
Enigme pour les secondes .
Libellés : Enigme
04 février 2010
La roue hexagonale .(version complètée)
Libellés : Enigme
27 janvier 2010
Cinq nombres et dix sommes .
2001, 2006, 2007, 2008, 2009, 2014, 2017, 2018, 2023 et 2025.
Quels sont ces cinq nombres ?
Libellés : Enigme
21 janvier 2010
2010 , année zéro .
Libellés : Enigme, Infos et actualités
20 janvier 2010
Le 2010 eme .
Quel est le 2010 eme chiffre de cette suite ?
Libellés : Enigme
13 janvier 2010
Neige à Saint-Malo .(version corrigée)
Quelques flocons sont tombés hier en Maine et Loire. Source de la photo
Libellés : Enigme, Messages aux classes de G.Marion, Récréation
04 janvier 2010
Un symbole pour la nouvelle année.
21 décembre 2009
Fourmi ravitailleuse .
La dernière fourmi du groupe décide d'aller ravitailler la fourmi chef et pour cela rejoint la tête de la colonne puis sa mission étant accomplie, retourne aussitôt à la queue de la colonne.
Sachant que, pendant cet aller-retour, la vitesse de cette fourmi est restée constante et que la colonne a parcouru 50 cm, quelle est la distance parcourue par la fourmi ravitailleuse ?
Libellés : Enigme
17 décembre 2009
Enigme pour les vacances .
Un nombre palindrome est un nombre entier non nul qui peut se lire de la même manière dans les deux sens (par exemple : 12 321).
S’ils sont rangés dans l’ordre croissant, le premier de ces nombres est 1 alors que 55 porte le numéro 14. On dit aussi que 55 est le 14ème nombre palindrome.
1) Quel est le 5ème nombre palindrome ?
2) Quel est le 20ème nombre palindrome ?
3) Donner le rang du premier nombre palindrome à 3 chiffres, puis celui du dernier nombre palindrome à 3 chiffres.
4) Un jeune mathématicien, âgé de 22 ans, spécialiste des nombres palindromes, protège les résultats de ses recherches dans un coffre-fort dont la combinaison comporte quatre chiffres. Pour se souvenir de la combinaison d’ouverture du coffre, le chercheur utilise le seul nombre palindrome dont le quotient par son rang dans la liste des nombres palindromes est égal à son âge .
Quelle peut bien être la combinaison choisie par le savant ?
Libellés : Enigme
08 décembre 2009
Soldes mathématiques.
Un professeur de mathématiques effectue trois remises successives sur une semaine de cours particuliers facturée initialement 300 € et la propose finalement à 222,87 €.
Quels sont les pourcentages des trois remises appliquées, sachant qu’il s’agit de valeurs entières ?
Libellés : Enigme
31 octobre 2009
Enigme pour les Secondes (et les autres peut-être)
Libellés : Enigme, Messages aux classes de G.Marion, Récréation
30 octobre 2009
Enigme pour les secondes .
1*2*3*4+1
2*3*4*5+1
3*4*5*6+1
4*5*6*7+1
Qu'y a t-il de remarquable ?
En est-il toujours ainsi ?
Libellés : Enigme
20 octobre 2009
Joyeuse énigme .
Pour quels entiers n > 0,tout polynôme de degré n est-il jovial?
Libellés : Enigme
07 octobre 2009
Enigme pour les sixième .
01 octobre 2009
Cryptarithme.
Aucun nombre ne peut commencer par un zéro;les accents sont sans incidence;idéalement,il n'y a qu'une solution,mais ce n'est pas toujours le cas.
Les plus beaux cryptarithmes sont évidemment ceux qui forment des phrases ayant un sens.Le but du casse-tête est,à partir de l'opération en lettres,de retrouver la correspondance entre lettres et chiffres
EPOUX + EPOUSE = COUPLE
MI + RE + DIESE + MI + RE + DIESE + MI = ELISE(on reconnaît dans le dernier le tout début de la "lettre à Élise" de Beethoven)
Page (Source) pour les résoudre.
Libellés : Enigme, Récréation
30 septembre 2009
Nombre carrément carré .
Le premier de ces nombres est :
49= 7² ; 4=2² et 9=3²
Le suivant est 1681= 41² ; 16= 4² ; 81=9²
Les suivants sont :
144 400 = 380²
225 625 = 475²
256 036 = 506²
324 900 = 570²
576 081 = 759²
24 019 801 = 4901²
Libellés : Enigme, Récréation
24 septembre 2009
Anniversaire géométrique .
Dans ma famille,les anniversaires ont lieu en automne ou en hiver,peu de temps avant les fêtes de fin d'année : Cette accumulation est un peu gênante;pas tant que cela en réalité,mais en revanche,les débuts d'année sont peu festifs.(oui,oui,cela a été mal calculé!)Libellés : Enigme, Récréation
18 septembre 2009
Puissante énigme à solution carrée
Pour quel(s) entier(s) n > 0 la somme des puissances huitième,onzième et n-ième de 2
(2^8+2^11+2^n)
est-elle le carré d’un entier?
Libellés : Enigme
09 septembre 2009
Enigme du 9 septembre 2009 :
Libellés : Enigme
11 août 2009
Arithmétique pour les vacances.
alors que 7^7 divise (a+b)^7-a^7-b^7.
Extrait du problème 2 de la 25ème Olympiade Mathématique Internationale (Prague, 1984).
Aide :
Factoriser
(a + b)7 – a7– b7
Libellés : Enigme
25 juin 2009
Enigme pour les vacances
Un triangle équilatéral est inscrit dans un rectangle
(j'ai bien dit rectangle) avec lequel il partage un sommet.
Notons A, B et C, les aires des trois triangles complémentaires, tel qu'illustré ci-contre.
Démontrez que A + B = C.
Source : Centrale des maths
Libellés : Enigme
18 juin 2009
Arithmétique .
Libellés : Enigme, Messages aux classes de G.Marion
16 juin 2009
Un nombre .
Dîtes tout ce que vous pouvez sur ce nombre .
Libellés : Enigme, Messages aux classes de G.Marion
08 mai 2009
Pour les futurs secondes
Libellés : Enigme
24 avril 2009
Pour les élèves de seconde
21 avril 2009
Calcul algébrique.
Libellés : Enigme
02 avril 2009
Géométrie
Une équerre se déplace dans un plan vertical avec les deux sommets A et B de « l’hypoténuse » qui coulissent le long de deux axes perpendiculaires.
Quel est le lieu géométrique décrit par le sommet M de l'angle droit lors du déplacement ?
cliquer sur l'image pour l'agrandir
Libellés : Enigme
01 avril 2009
Géométrie d'avril .
Libellés : Enigme, Récréation
26 mars 2009
Année complexe .
Libellés : Enigme
21 mars 2009
Insolite éponge de Menger.
2) Lundi, on reparlera origami
Libellés : Enigme, Infos et actualités, Récréation
14 mars 2009
2009 : Damnée arithmétique !
Libellés : Enigme
10 mars 2009
2009: Le retour
Libellés : Enigme
07 mars 2009
Deux nombres
05 mars 2009
Si par hasard , sur...
Prop. 2 : Monsieurmath choisit "au hasard" une des 5 places qui restent. L'événement est réalisé si Monsieurmath choisit la place libre sur le banc où est installée Missmath et p = 1/5.
Nota Bene :
On négligera l'influence du vent fripon .
Libellés : Enigme
26 février 2009
Enigme pour retraité.
Libellés : Enigme
12 février 2009
2009 encore (et toujours sans calculatrice)
Libellés : Enigme
30 janvier 2009
La somme des chiffres de mon cube
Quel nombre suis-je?
Libellés : Enigme
16 janvier 2009
Enigme pour amateurs de programmation
Libellés : Enigme
14 janvier 2009
Le chiffre manquant
Libellés : Enigme
07 janvier 2009
Sans calculatrice s.v.p.
22 décembre 2008
Mon numéro de carte bancaire.
Pouvez vous le retrouver ? J'en ai besoin pour les cadeaux de Noël.
Libellés : Enigme
05 décembre 2008
Enigme pour les secondes :37
Libellés : Enigme
20 novembre 2008
Enigmath 2008 : Du 17 novembre 2008 au 20 février 2009
Dans le cadre de la Fête de la Science 2008, vous pouvez tester vos connaissances en mathématiques en jouant à Enigmath... une centaine de cadeaux à gagner !
Il s'agit d'un Quizz de Mathématiques GRATUIT ne nécessitant que des connaissances élémentaires.
Les objectifs principaux sont de mettre en valeur auprès du grand public la place occupée par les mathématiques dans notre vie de tous les jours, et d'aborder des aspects de la recherche en mathématiques ou liés aux mathématiques, tout en permettant aux participants de s'évaluer sur des questions de mathématiques simples.
Pour jouer à Enigmath 2008, c'est ici!
Libellés : Enigme
14 novembre 2008
Quel est mon âge ?
11 novembre 2008
Où est l'erreur ?
x²+1 = 0.
Celle-ci équivaut à :
(x+1)² - 2x = 0 , ou encore :
(x+1)² = 2x .
Comme un carré est toujours positif ou nul,on en déduit que x est positif ou nul.
(Déduction n° 1)
Mais notre équation peut aussi s'écrire:
(x-1)² + 2x =0 , soit encore :
(x-1)² = - 2x
Comme un carré est toujours positif ou nul,on en déduit que - x est positif ou nul,
donc que x est négatif ou nul
(Déduction n° 2)
En comparant les deux déductions précédentes,on conclut :
x = 0 .
Pourtant 0 n'est pas solution de l'équation de départ !
Libellés : Enigme, Messages aux classes de G.Marion, Récréation
07 novembre 2008
Championnat des jeux mathematiques (organisé par la fédération française des jeux mathématiques).
Vous pouvez participer en ligne sur www.ffjm.org ou imprimer les énoncés
bulletins-réponses et envoyer le tout avant le 1er janvier 2009 à FFJM, 8
rue Bouilloux-Lafont, 75015 Paris.
La FFJM organise également un championnat de jeux littéraires et un combine
jeux mathématiques-jeux littéraires (voir sur http://www.ffjm.org)
Ci-dessous un des énoncés des 16 problèmes à résoudre pour participer aux quarts de finale dans la catégorie lycée:
LA SUITE DE FIBO ET DE GÉO:
Fibo choisit trois nombres entiers strictement positifs comme premier,
deuxième et troisième termes d’une suite.
En multipliant le troisième par la somme du deuxième et du premier,
Géo calcule le quatrième terme de la suite.
En multipliant le quatrième par la somme du troisième et du
deuxième, Géo obtient le cinquième terme de la suite, 2008.
Quels sont, dans l’ordre, les trois nombres choisis par Fibo ?
Libellés : Enigme, Messages aux classes de G.Marion
18 octobre 2008
Mille et une soustractions pour un krach numérique.
est divisible par 2003.
Libellés : Enigme
17 octobre 2008
Combien de zéros ?
(A) 10
(B) 11
(C) 20
(D) 24
(E) 25
Libellés : Enigme
07 octobre 2008
Quel est mon âge ?
"L'an prochain, mon âge sera divisible par 2. Dans deux ans, mon âge sera divisible par 3. Dans trois ans, mon âge sera divisible par 4. Dans quatre ans, mon âge sera divisible par 5 et je ne suis pas encore centenaire ."
Quel est mon âge ?
Libellés : Enigme
06 octobre 2008
Trois sphères pour trois lettres.
Intersection de 2 sphères :
Un cercle (en rouge)
Intersection de 3 sphères :
2 points (en noir)
Si un des points n’est pas à la surface de la Terre, votre position est l'autre point.
Trois lettres ?
P.S. On peut survivre sans maths , mais pas toujours !
Libellés : Enigme, Images mathématiques
05 octobre 2008
Un équation du second degré avec 3 solutions ?
Dans le cas réel qui seul nous concernera ici, une équation de degré 2 possède donc au plus 2 solutions différentes.
Souvenez-vous, pour l’équation ax² + bx + c = 0, les racines
sont données par :
x' = (-b + √Δ)/2a ; x" = (-b - √Δ)/2a
où Δ = b² - 4ac
Pourtant, voici une exception à cette règle. Considérons trois nombres réels a, b et c fixés et deux à deux distincts
(si vous le souhaitez, prenez a = 1, b = 2, c = 3). Analysons l’équation suivante :
[(x − a)(x − b)]/[(c − a)(c − b)]+ [(x − b)(x − c)]/[(a − b)(a − c)]+[ (x − a)(x − c)]/[(b− a)(b − c)] = 1
C’est une équation de degré 2 en l’inconnue x car c’est une somme, chaque terme étant un polynôme de degré 2.
Le nombre a est solution de l’équation car, quand on remplace x par a, le premier terme s’annule, de même que le troisième, alors que le second prend la valeur 1. Notons qu’aucun dénominateur ne s’annule, nous respectons bien les règles de calcul qu’impose ce genre de manipulations.
Le nombre b et le nombre c, pour des raisons analogues, sont aussi solutions de cette équation qui possède donc trois solutions. Puisque a, b et c ont été supposés distincts, nous avons donc une équation du degré 2 possédant 3 solutions différentes.
Est-ce la trace d’un paradoxe au coeur de l’algèbre élémentaire, et faut-il entreprendre le rappel des millions de livres de mathématiques qui mentionnent l’énoncé du théorème fondamental de l’algèbre ?
Ou bien y a t-il une petite erreur quelque part ?
Extrait de :
Paradoxes par Jean-Paul Delahaye
Libellés : Enigme, Messages aux classes de G.Marion
17 septembre 2008
Une curieuse propriété.
La séquence des sept entiers consécutifs 9, 10, 11, 12, 13, 14 et 15 a la curieuse propriété que les sommes des chiffres de leurs carrés respectifs 81, 100, 121, 144, 169, 196 et 225 sont elles-mêmes des carrés parfaits : 9, 1, 4, 9, 16, 16 et 9.
Existe-t-il d'autres séquences de 7 nombres entiers consécutifs positifs dont la somme des chiffres de chacun de leurs carrés est elle-même un carré parfait ?
Trouvé sur le site Diophante.fr
Libellés : Enigme
13 septembre 2008
Mathématique ou magique ? : L'escalier en spirale de Santa Fe, Nouveau Mexique, U.S.A.
A la fin du XIX° siècle, à Santa-Fé (Nouveau Mexique, Etats-Unis), un charpentier réalise un escalier à la tenue inexplicable.Cet escalier en colimaçon est un chef d’œuvre, aussi magnifique qu’étonnant. Il fait deux tours complets (2 x 360°) sur lui-même mais il n’y a aucun pilier pour le soutenir ... il a cependant été utilisé quotidiennement pendant plus de cent ans .
Les architectes ne comprennent pas comment il a été construit, ni comment il est demeuré en aussi bon état après quasiment un siècle d’utilisation.
Un "mystère" qui attire plus de 250 000 visiteurs chaque année.
Libellés : Art et mathématiques, Enigme
28 août 2008
Crapahuter fait -il maigrir ?
Je suis parti une semaine marcher dans les montagnes du Pays BasqueMontée de la mythique Rhune * pour commencer et de plus en plus haut ensuite , en augmentant le dénivelé progressivement .
(le lien pointe vers un fichier KML ouvrable dans Google Earth).
Triple objectif:
Soigner l'âme , vider le cerveau des pollutions qu'il a dû subir pendant une dure année et moins noble je l'avoue , lutter contre l'obésité rampante qui guette impitoyablement le privilégié que je suis .
Pour vérifier que le troisième objectif avait bien été atteint , sûr du résultat après avoir sué sang et eau pendant huit jours , je me suis pesé dès mon retour au bercail.
Et là , catastrophe , les chiffres ont parlé : Malgré deux crans de ceinturon gagnés ,le verdict tomba comme une douche froide : Un kilo de plus qu'au départ!
ô rage , ô désespoir , ô ma graisse ennemie ! (pas facile d'être aussi drôle que Missmath)
Alors , j'ai voulu en avoir le coeur net et j'ai interrogé les moteurs de recherche :
Question volume , on va dire que le bilan est neutre ; je l'ai vérifié en prenant mon bain ; quand je plonge dans ma baignoire , le niveau de l'eau monte ni plus , ni moins qu'avant : Logique , les quelques litres gagnés au niveau de l'abdomen sont compensés par la très forte augmentation du diamètre de mes cuisses et de mes bras . Mais alors comment expliquer la prise de poids ?
Une fois de plus c'est mathématique :
La densité de l'eau est 1 par définition et celle de l'huile est de 0,8 environ.
Le muscle est pauvre en graisse, sa densité se rapproche de celle de l'eau.
Le tissu graisseux en général est pauvre en eau, sa densité tend vers celle de l'huile.
Question :
Sachant que mon poids a augmenté de un kilo et que mon volume est resté globalement constant , combien de litres de graisses ai- je transformé en muscles ?
* Avec ses 900 mètres d'altitude, la Rhune (larra un : lieu de pâturage en basque) pourrait faire pâle figure auprès des seigneurs des Pyrénées, mais elle en est pourtant un symbole.
Fréquentée dès la préhistoire, la montagne abonde en tumuli, en cromlechs et en dolmens. Au cours des siècles, les bergers y guidèrent les troupeaux de manech, une race locale de brebis, aux cornes tire-bouchonnées. Le pottock, petit cheval endémique, vit aussi en semi-liberté sur les flancs de la Rhune.
Cet incomparable belvédère où passe la frontière fut de tous temps révéré, et l'on y place certains des sabats des "sorcières" basques, traquées et brûlées au début du 17e s. par le sadique Conseiller de Lancre. Plus tard, l'Impératrice Eugénie, séjournant à Biarritz, lança la mode des excursions à La Rhune.
Libellés : Enigme, Récréation
27 juin 2008
Pour les MPSI (maths sup)
Libellés : Enigme
22 mai 2008
Magie ?
Ex: 5, 2, 7, 9, 16, 25, 41, 66, 107, 173
Demandez-lui quel est le 7ème nombre.
Immédiatement vous pouvez donner la somme des dix nombres.
Comment ?
Libellés : Enigme, Récréation
20 mai 2008
"Recrutement chez google" : Solution du problème du 19 mai.
19 mai 2008
Recrutement chez Google : Entraînez vous !
Pour sélectionner ses futurs employés , Google lance des “chasses au trésor” sur internet. Celle-ci, commence assez fort: Si le robot ci-dessus ne peut aller que vers la droite ou vers le bas, combien y a t-il de chemins distincts qui le mènent au but ?
Et si le damier compte 39*33 cases ?
Libellés : Enigme
03 mai 2008
La vitesse de la pétrolette.
À quelle vitesse Valentin roule-t-il?
Libellés : Enigme
29 avril 2008
Les enigmes de la galerie Cecconi
Toutes les semaines une énigme en image comme celle ci-contre et la solution la semaine suivante ; c'est ici
Libellés : Enigme
27 avril 2008
Pour les élèves de Seconde.
Il traîne en chemin, fait de longues pauses pour apprécier la nature en ce joli mois de mai.
Résultat : Il n'a parcouru son trajet qu'à une vitesse de 10 km/h.
Malheureusement, il se fait tard et notre cycliste décide de rentrer par le même chemin.
Pour arriver avant la nuit (il n'a pas de phares) , il faut que sa vitesse moyenne sur toute la promenade - c'est-à-dire aller et retour - soit de 20 km/h.
A quelle vitesse devra-t-il rouler pour le trajet retour ?
Libellés : Enigme, Récréation
07 avril 2008
Savoir qu’un autre ne sait pas peut permettre de conclure ! Exemple:
Jacques dit « Je ne sais pas quel est N ».
Dans un second temps, donc après avoir pris en compte la réponse de Jacques, Jules dit:
« Je ne sais pas moi non plus ».
Combien N a-t-il de diviseurs ?
La solution ci-dessous ( dans quelques jours seulement !)
solution-enigme-diviseurs.doc
Libellés : Enigme
26 mars 2008
Le paradoxe des anniversaires.
Quelle est la probabilité que cela se produise?
La solution est ci-dessous ( seulement après avoir bien cherché ! )
paradoxe%20-anniversaires%20-solution.doc
Libellés : Enigme, Messages aux classes de G.Marion
19 mars 2008
Les maris jaloux
Trois maris jaloux se trouvent avec leurs femmes au passage d’une rivière, et rencontrent un bateau sans batelier ; ce bateau est si petit, qu’il ne peut porter plus de deux personnes à la fois. On demande comment ces six personnes passeront, de telle sorte qu’aucune femme ne demeure en la compagnie d’un ou de deux hommes, si son mari n’est présent.
La solution est ci-dessous
maris-jaloux.doc
Libellés : Enigme
16 février 2008
Enigme pour les vacances :Logique papoue
En Papouasie, il y a des “papous” et des “pas papous”. Parmi les “papous”, il y a des “papas papous” et des “papous pas papa”. Mais il y a aussi des “papas pas papous” et des “pas papous pas papas”.
De plus, il y a des “papous pas papas à poux” et des “papas pas papous à poux”. Mais n’y a pas de “papas papous à poux” ni de “pas papous pas papas à poux”. Sachant qu’il y a 240 000 poux ( en moyenne 10 par tête ) … et qu’il y a 2 fois plus de “pas papous à poux” que de “papous à poux”, déterminer le nombre de “papous pas papas à poux” et en déduire le nombre de “papas pas papous à poux”.
Libellés : Enigme, Récréation
09 février 2008
Le reste de la division de N par 5.
On choisit un nombre entier N entre 1 et 12. On indique à Jacques la somme de tous les diviseurs de N. Jacques dit alors :
« Je ne sais pas quel est le nombre N ».
Trouver le reste de la division de N par 5.
Rappelons que, parmi les diviseurs d'un nombre, il y a toujours 1 et lui-même. Par exemple, les diviseurs de 8 sont 1, 2, 4 et 8 et la somme des diviseurs de 8 est 15.
Libellés : Enigme
14 janvier 2008
Le mouton.
Sur cette île , chaque jour et dans cet ordre, chaque loup tue un mouton, chaque mouton tue un serpent et chaque serpent tue un loup.Après dix jours il ne reste plus sur l’île qu’un mouton et aucun autre animal .
Combien y avait-il d’animaux de chaque espèce au départ ?
Libellés : Enigme
09 janvier 2008
Le nombre de pages du livre.
Les pages d'un livre sont numérotées de 1 à n .
(on rappelle que la page numérotée 1 est toujours une page de droite).
On additionne toutes les pages et on trouve un total égal à 2003. Mais deux pages numérotées sont restées collées et leurs numéros n'ont pas été comptés.
N.B. Vous avez droit aux calculatrices
Libellés : Enigme
25 décembre 2007
Enigme pour 2008
par 22 ?
et par 21 ?
Libellés : Enigme, Récréation
23 novembre 2007
Le chemin le plus court
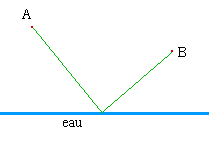
Quel est le trajet le plus court ?
Ne cliquez pas ici, c'est de la pub
Libellés : Enigme
05 novembre 2007
Avis de recherche
C'est un nombre de quatre chiffres.
Ses deux chiffres de gauche sont égaux
Ses deux chiffres de droite aussi.
Libellés : Enigme
04 novembre 2007
Enquête mathématique
Pour tout i > 0,
- Si Ui est pair alors U i+1 = Ui / 2
- Si Ui est impair alors Ui+1 = 3×Ui + 1
Dans cette suite de Syracuse , Un = 1 et U1 = 6144 ; le numéro où vous devez vous rendre est Un-9.
A quelle numéro avez-vous rendez-vous ?
Libellés : Enigme, Messages aux classes de G.Marion
31 octobre 2007
Enigme d'Halloween
Un vampire de facture classique doit sucer le sang d’un être humain chaque mois, faisant de celui-ci un vampire qui doit à son tour trouver une nouvelle victime par mois.
Question : Combien de temps aurait-il fallu à un seul vampire pour contaminer les 537 millions d’habitants qui vivaient sur Terre aux alentours des années 1600 ?
Libellés : Enigme, Récréation
26 octobre 2007
Enigme du 19 octobre : Il y avait une solution bien plus courte que les autres !
Rappel de l'énoncé
Vous voulez acheter un billet de loterie. Le buraliste, logicien comme
tous les buralistes, vous en présente cinq numérotés de 1 à 5 et vous déclare :
a) si 5 est perdant, alors 1 est gagnant ;
b) si 4 est perdant, alors 2 est gagnant ;
c) si 3 est perdant, alors 5 aussi ;
d) si 1 est gagnant, alors 2 aussi ;
e) si 3 est gagnant, alors 4 est perdant.
Quel billet choisissez-vous ?
Supposons le billet 3 gagnant:
Alors , d'après e) , le 4 est perdant et d'après b) , le 2 est gagnant
Supposons au contraire que le billet 3 est perdant:
Alors , d'après c), le 5 est perdant et par conséquent d'après a) , le 1 est gagnant et d'après d) , le 2 est gagnant
Conclusion : Le billet 2 est toujours gagnant
(Il reste à justifier que c'est le seul billet toujours gagnant)
Libellés : Enigme
22 octobre 2007
Solution à l'énigme du 19 octobre
(postée sur le blog dimanche 21 octobre à 14 heures par ln et fred : pari gagné)
Enoncé
Vous voulez acheter un billet de loterie. Le buraliste, logicien comme
tous les buralistes, vous en présente cinq numérotés de 1 à 5 et vous déclare :
– si 5 est perdant, alors 1 est gagnant ;
– si 4 est perdant, alors 2 est gagnant ;
– si 3 est perdant, alors 5 aussi ;
– si 1 est gagnant, alors 2 aussi ;
– si 3 est gagnant, alors 4 est perdant.
Quel billet choisissez-vous ?
Solution
A l'aide des données de l'énoncé, on n'obtient que 5 situations possibles parmi les 32 cas envisageables : Tous les autres cas contredisent les données de l’énoncé.
Les cinq cas possibles sont :
+1 +2 +3 -4 +5
+1 +2 +3 -4 -5
+1 +2 -3 +4 -5
+1 +2 -3 -4 -5
-1 +2 +3 -4+ 5
Le seul billet qui est gagnant dans chacun de ces cas est le billet 2 .
Libellés : Enigme
19 octobre 2007
Enigme
Vous voulez acheter un billet de loterie. Le buraliste, logicien comme
tous les buralistes, vous en présente cinq numérotés de 1 à 5 et vous déclare :
– si 5 est perdant, alors 1 est gagnant ;
– si 4 est perdant, alors 2 est gagnant ;
– si 3 est perdant, alors 5 aussi ;
– si 1 est gagnant, alors 2 aussi ;
– si 3 est gagnant, alors 4 est perdant.
Quel billet choisissez-vous ?
Libellés : Enigme
24 juin 2007
Enigme pour les vacances des élèves de seconde
En 1484, le mathématicien français Nicolas Chuquet présenta le jeu suivant dans son traité d’algèbre intitulé “Triparty en la science des nombres”.
Une personne lance trois dés ; je lui demande de doubler le résultat x de l’un d’eux au choix puis d’ajouter 5, de multiplier le tout par 5 et d’ajouter le résultat y d’un des deux autres dés ; de doubler et multiplier encore par 5, puis d’ajouter le résultat z du troisième dé et je lui demande le nombre obtenu.
Alors, je connais les valeurs de x , y et z .
Et vous ?
Libellés : Enigme
22 juin 2007
Enigme pour les vacances des élèves de première.
Otis Thyssen habite un immeuble de plus de 3 étages, de moins de 25 étages, sans sous-sol, et possédant un unique ascenseur.
On suppose que les allées et venues sont telles que l'appareil, lorsqu'il est à l'arrêt, a une chance sur deux d'être au rez-de-chaussée, et des probabilités égales d'être au premier étage, au deuxième étage, au troisième, etc..
Lorsque Otis sort de son appartement, et qu'il appelle l'ascenseur, alors que celui-ci est à l'arrêt, l'appareil parcourt en moyenne exactement deux fois plus de distance que lorsqu'on l'appelle du rez-de-chaussée ou du premier.
A quel étage habite Otis?
Aide: note n le nombre d'étages , p l'étage de l'appartement d'Otis,
E(Di ) l'espèrance de la distance parcourue lorsqu'on appelle l'ascenseur de l'étage n° i .
(L'espérance d'une variable aléatoire est la moyenne espérée de cette variable lorsqu'on répète un grand nombre de fois l'expérience)
Ainsi
E(Do)=(1/2) *0 +(1/2n)*1 +(1/2n)*2+ ... +(1/2n)*n = .....
Pour exprimer E(Dp) , tu envisageras 3 cas : L'ascenseur est au rez de chaussée,ou en dessous de l'étage p , ou au dessus de l'étage p
Libellés : Enigme
20 juin 2007
Enigme pour les vacances (pour les élèves de terminale)
Klomac et Barriton jouent avec Toutrouge. Ils lui demandent de choisir deux nombres entre 2 et 100. Toutrouge tend un papier à Klomac en lui indiquant qu'il s'agit de la somme de ces deux nombres. Puis il tend un papier à Barriton avec le produit de ces deux nombres. Suit un discours étonnant:
B : Ce produit ne me permet pas de déterminer quels sont ces deux nombres.
K: Je le savais!
B: Alors je connais ces 2 nombres.
K: Dans ce cas, moi aussi!
Quels sont ces deux nombres?
Libellés : Enigme
28 avril 2007
Solution à la très difficile énigme du 31 mars(énigme des moines)
L'énigme se passe dans un monastère très strict ou vivent 40 moines. Ces moines ont pour seule vocation la prière et il ne doivent absolument pas communiquer entre eux, ni par geste, encore moins par la parole. Ils ne peuvent même pas se regarder dans un miroir. Chaque jour, le père supérieur, qui est le seul à pouvoir parler, réunit les moines dans la salle de réunion pour les informer des nouvelles du jour. Une maladie très dangereuse et peut-être contagieuse vient d'arriver chez les moines, elle se caractérise par la présence de petites plaques rouges sur le visage, bien visibles mais non douloureuses. Elle ne provoque pas d'autres symptômes au début. Chaque moine ne peut donc pas savoir s'il est malade.
Le père supérieur décide de prévenir les moines. Lors de la réunion quotidienne, ils les informe donc que cette maladie est dangereuse, et ils demande qu'à la fin de chaque réunion, quand il le demandera, tous ceux qui se savent malades préparent leur valises et partent du monastère.
A la fin de cette réunion, le père supérieur demande: "Que tous ceux qui se savent malades se lèvent et s'en aillent". Mais personne ne se lève.
Le lendemain, à la fin de la réunion, le père supérieur demande: "Que tous ceux qui se savent malades se lèvent et s'en aillent". Mais personne ne se lève.
Le surlendemain, à la fin de la réunion, le père supérieur demande: "Que tous ceux qui se savent malades se lèvent et s'en aillent". A ce moment là, tous les moines qui sont malades se lèvent et s'en vont. Combien sont ils?
Supposons qu'un seul moine soit malade. Lors de l'annonce du père supérieur, celui-ci constate forcément qu'aucun autre moine n'est malade, mais comme la maladie frappe bel et bien le monastère, c'est que lui même est malade est c'est le seul. Il devrait donc partir après la première annonce du père supérieur.
S'il y a 2 moines malades, chacun des deux moines malades voit qu'un autre est malade. Mais ils ne savent pas si eux mêmes sont malades. Ils attendent donc la fin de la première annonce. Aucun d'eux ne se lève car il ne savent pas s'ils sont malades. Mais à la fin de la réunion, comme aucun d'eux ne s'est levé, ils savent qu'il y a plus qu'un seul malade, car sinon on serait dans le cas précédent et l'unique malade serait parti à la fin de la première réunion. Ils sont donc bien tous les deux malades et, le lendemain, dès l'annonce du père supérieur ils peuvent se lever et partir car ils savent maintenant qu'ils sont les 2 seuls malades.
Faisons l'hypothèse que s'il y avait n malades, il pourraient partir juste après la nième annonce du père supérieur car ils sauraient tous qu'ils sont malades.
Supposons qu'il y ait n+1 malades, chacun d'eux en voit n autres, mais ne savent pas s'il y a n malades ou bien n+1 car ils ne savent rien en ce qui les concerne eux-même. Ceux-ci doivent donc attendre la fin de la réunion du nième jour pour savoir s'il sont malades. S'ils étaient n, ils seraient partis à la fin du nième jour d'après l'hypothèse. S'ils ne sont pas partis le nième jour, c'est donc qu'ils sont n+1, et ils peuvent donc partir juste après la (n+1) ième annonce. Comme l'hypothèse est vraie pour n=1, et que nous venons de vérifier la récurrence, l'hypothèse est démontrée.
En conclusion, tel qu'est posé l'énoncé, il y a 3 moines malades. Et le fait qu'ils soient 40 au départ n'est là que pour embrouiller les esprits .
Libellés : Enigme
31 mars 2007
Enigme pour les vacances (pour les Terminales S)
L'énigme se passe dans un monastère très strict ou vivent 40 moines. Ces moines ont pour seule vocation la prière et il ne doivent absolument pas communiquer entre eux, ni par geste, encore moins par la parole. Ils ne peuvent meme pas se regarder dans un miroir. Chaque jour, le père supérieur, qui est le seul à pouvoir parler, réunis les moines dans la salle de réunion pour les informer des nouvelles du jour.
Une maladie très dangereuse et peut etre contagieuse vient d'arriver chez les moines, elle se caractérise par la présence de petites plaques rouges sur le visage, bien visibles mais non douloureuses. Elle ne provoque pas d'autres symptomes au début. Chaque moine ne peut donc pas savoir s'il est malade.
Le père supérieur décide de prévenir les moines. Lors de la réunion quotidienne, ils les informe donc que cette maladie est dangereuse, et ils demande qu'à la fin de chaque réunion, quand il le demandera, tous ceux qui se savent malades préparent leur valises et partent du monastère.
A la fin de cette réunion, le père supérieur demande: "Que tous ceux qui se savent malades se lèvent et s'en aillent". Mais personne ne se lève.
Le lendemain, à la fin de la réunion, le père supérieur demande: "Que tous ceux qui se savent malades se lèvent et s'en aillent". Mais personne ne se lève.
Le surlendemain, à la fin de la réunion, le père supérieur demande: "Que tous ceux qui se savent malades se lèvent et s'en aillent". A ce moment là, tous les moines qui sont malades se lèvent et s'en vont. Combien sont ils?
(La solution sera en ligne fin avril)
Bonnes vacances!
Libellés : Enigme
25 mars 2007
Partage d'un carré :
Peut-on partager la surface d'un carré en quatre triangles isocèles non rectangles ?
Libellés : Enigme
19 février 2007
Extrait des Olympiades mathématiques 2006
Quel est le nombre total de chiffres écrits pour la pagination ?
Combien de fois le chiffre 7 a- t-il été utilisé ? Et le chiffre 0 ?
Voir la solution (seulement après avoir bien cherché)
Libellés : Enigme
15 février 2007
Trouvez l'erreur
Un homme est condamné à mort le samedi .Le juge prononce la sentence:
« Vous serez exécuté un des 7 matins de la semaine à venir mais vous ne connaîtrez le jour de l'exécution que le matin où elle aura lieu. »
Le condamné réfléchit puis éclate de joie:
« je ne peux pas être exécuté le dimanche , dernier jour de la semaine, car je serais alors vivant le samedi à midi et je connaîtrais par conséquent le jour de mon exécution.
je ne peux pas être exécuté le samedi , car je serais alors vivant le vendredi à midi. Comme l'exécution ne peut avoir lieu le dimanche, je saurais alors qu'elle est fixée au samedi , ce qui viole encore la convention.
Ainsi en poursuivant le raisonnement de jour en jour , je démontre que l'exécution ne peut avoir lieu ni le vendredi , ni le jeudi, ni le mercredi, ni le mardi.
Il ne reste plus que le lundi.
Par le fait même que j'en arrive à cette conclusion , ce jour est également exclu. La sentence est inapplicable !!! »
Libellés : Enigme
06 février 2007
Bizarre, bizarre !
24 janvier 2007
Enigme
18 décembre 2006
Cherchez l'erreur
A= 1+2+4+8+16+32+64...
Alors
2A =2+4+8+16+32+64+128...
et
2A+1 = 1+2+4+8+16+32+64+128...
On a donc
2A+1=A
D'où A=-1
Or A est une somme de termes positifs. Comment peut-il être alors négatif?
Libellés : Enigme
08 décembre 2006
Mot de passe oublié
Elle se rappelle uniquement qu’il s’agit d’un nombre un peu particulier compris entre 1000
et 2 milliards: il est à la fois le carré d’un nombre entier, le cube d’un nombre entier et la puissance cinquième d’un nombre entier.
Marie se désespère : elle essaie des centaines de nombres sans succès. Elle se décide enfin à appeler son amie Sophie qui est passionnée par les mathématiques.
Cette dernière écoute toute l’histoire, réfléchit un instant puis s’exclame : « Il n’y a qu’un nombre qui vérifie toutes ces conditions ! Ce nombre est … ».
Quel est le nombre recherché par Marie ?
Libellés : Enigme
