23 novembre 2007
Le chemin le plus court
Je parts de A pour aller en B en passant me baigner.
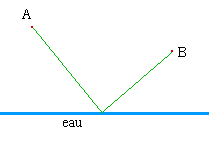
Quel est le trajet le plus court ?
Ne cliquez pas ici, c'est de la pub

Quel est le trajet le plus court ?
Ne cliquez pas ici, c'est de la pub
Libellés : Enigme
Comments:
Links to this post:
<< Home
que je suis bête
en fait je dirai qu'il faut allé tout droit vers la mer et ensuite tou droit vers B
mais je vais reflechir a une methode pour prouver tt ca
Hervé
en fait je dirai qu'il faut allé tout droit vers la mer et ensuite tou droit vers B
mais je vais reflechir a une methode pour prouver tt ca
Hervé
Il faut prendre le symétrique de A par rapport à la droite bleue (le symétrique est nommé A'), et le relier A' à B.
Prendre le symétrique de B par rapport à la droite bleue(symétrique nommé B'), puis relier B' à A.
Le chemin le plus court est tracé ;)
Alors, c'est ça?
Prendre le symétrique de B par rapport à la droite bleue(symétrique nommé B'), puis relier B' à A.
Le chemin le plus court est tracé ;)
Alors, c'est ça?
C'est un peu mal expliqué mais je suis en 4eme et les démonstration c'est pas trop mon truc mais l'idée est (peut être) là. :P
Alors...Comme je le disais tout à l'heure, les démonstrations ne sont pas mes points forts. Mais je vais y réfléchir :)
Peut être y a t-il un rapport avec Pythagore?
Ou peut être car A' prime étant le symétrique de A, on cherche le chemin le plus court de B à A' et pareil avec B' et A?
Nan sinon je n'ai aucune idée pour le moment mais je vais réfléchir :D
Peut être y a t-il un rapport avec Pythagore?
Ou peut être car A' prime étant le symétrique de A, on cherche le chemin le plus court de B à A' et pareil avec B' et A?
Nan sinon je n'ai aucune idée pour le moment mais je vais réfléchir :D
J'ajoute : le chemin le plus court est la droite. Il suffit donc que les angles formés par les droites et le plan d'eau soient égaux !
Enregistrer un commentaire
Links to this post:
<< Home






